Una función cuadrática es una función polinómica definida como:

Una función cuadrática es aquella que puede escribirse de la forma: f(x) = ax2 + bx + c donde a, b y c son números reales cualquiera y a distinto de cero ya que si es cero nunca será una parábola. Este tipo de funciones tiene como característica que cuando a>0 el verticé de la parábola se encuentra en la parte inferior de la misma y cuando a<0 el vértice se encuentra el la parte superior.
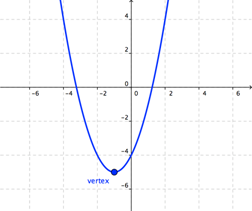
El vértice es el punto más alto o más bajo de la curva, dependiendo si la U se abre hacia arriba o hacia abajo. En el caso de que la parábola abra hacia arriba, el vértice será su punto más bajo; y una parábola que abre hacia abajo, tendrá un vértice en su punto más alto.
-b/2(a)
Eje de Simetría
El eje de simetría de una parábola es una recta que divide simétricamente a la curva, es decir, intuitivamente la separa en dos partes congruentes.Puede ser entendido como un espejo que refleja la mitad de la parábola en cuestión.
La ecuación asociada al eje de simetría viene dada por la relación:
c - b2/4(a)
Raíces
La raíces de una función cuadrática son aquellos valores de x que anulan la función (el valor de la función es cero, f(raíz)=0)

Las podemos encontrar usando la fórmula cuadrática.